Hello! This is Heba on the world’s slowest computer to
explain the key concepts in the Circular Function unit.
Arc Length
S= Arc Length
r= radius
θ= angle MEASURED IN RADIANS
The formula s=rθ can measure the arc length of a circle.
But, the angle MUST be measured in radians (if it's in degrees you'll have to convert it) and the arc length and the radius must be in the same units.
Example:
If the arc length is 81 cm and the radius is 27 cm, find the measure of the central angle to the nearest tenth of a degree.
Equation:
s=rθ
radius = 27 cm
S= 81 cm
1)Manipulate the equation to find the angle
s=rθ
θ=s/r
2) Plug in the variables
θ=81cm/27cm
θ= 3 radians
3) convert radians to degrees
3 (180 degrees/ π)
=171.8873385 dgr
=171.9 dgr
The Unit Circle

-has its centre at the origin
-has a radius of unit 1
-standard position starts at (1,0)
Equation of a unit circle:
x^2+y^2=1
What is positive distance?
Measured in counterclockwise direction
Negative Distance?
Measured in Clockwise direction
What is P(θ)?
-It is used to indicate where the terminal arm intercepts the unit circle.
- every arc length on the unit circle has a unique P(θ)
-P(θ) can also be defined as P(x,y)
SIN, COSIN, TANGENT on the unit circle

On the unit graph:
the y-axis = sin
x-axis=cos
P(θ)= (x,y) = (cosθ, sinθ)
Remember if r=1
sinθ=o/h = y/1=y
cosθ=a/h=x/1=x
tanθ=o/a=tanθ=y/x=sinθ/cosθ
therefore, P(x,y)=P(cosθ, sinθ) and since x^2+y^2=1 then cos^2+sin^2=1
Note: This equation is for a circle with centre at the orgin and a radius other than 1 would be x^2+y^2=r^2
CAST RULE:

CAST rule can help us identify which trigonometric function is positive at each quadrant.
EXAMPLE: Given that sinθ=-4/5 and cosθ=3/5 in which quadrant does θ lie?
Remember the CAST rule, if sinθ is negative and cosθ is positive than then θ must lie in quadrant 4.
Example 3: Determine the expression of the circle with centre at the origin and the radius of 2.
Remember, if the radius is bigger than 1 the equation becomes x^2+y^2=r^2.
x^2+y^2=4
Special Right Triangles:
Determining the exact values of trigonometric ratios of any multiples of 0 dgr, 30 dgr, 45 dgr, 60 dgr, 90 dgr.

There is a trick from India to remember the trigonometric ratios for special right triangles:
0 1 2 3 4
√0/4 √1/4 √2/4 √3/4 √4/4
sinθ 0 1/2 √2/2 √3/2 1
cosθ 1 √3/2 √2/2 1/2 0
tanθ 0 1/√3 1 √3 0 (UNDEFINED)
QUADRANTAL ANGLES

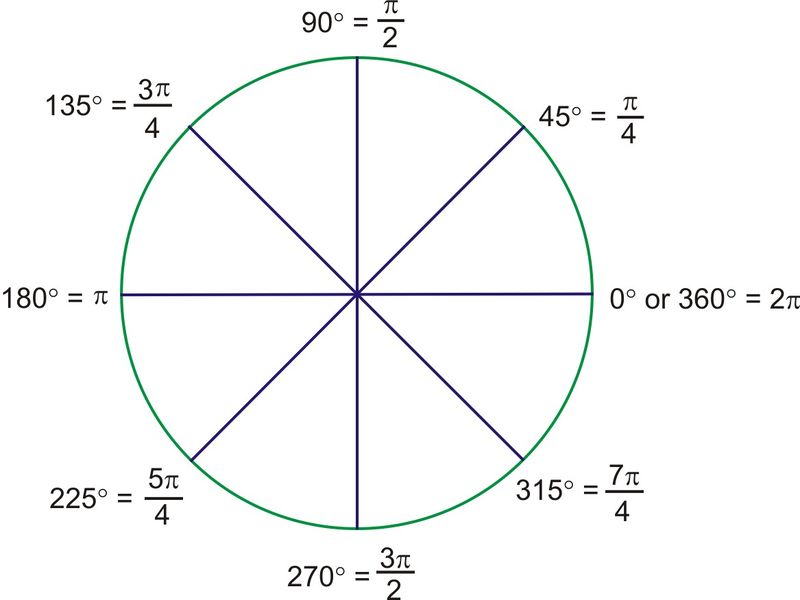
Example : Multiples of π/3
a. on a diagram of the unit circle, show the integral multiples of π/3 in which can be bigger and equal to zero or smaller than or equal to 2π

Note: 3π/3 does not count because it can reduced so it is NOT an integral multiple
b. what are the exact coordinates of each point P(theta) in part a
P(π/3)=(1/2, root 3/2)
(Cast rule so values are positive in Q1)
P(2π/3)= (-1/2, r3/2)
(Cast rules so cosin is negative Q2)
P(4π/3)=(-1/2,-r3/2)
(Cast rule so all values are negative in Q3)
P(5π/3)=(1/2, -r3/2)
(Cast rule so sin is negative in Q 4)
c.Identify any patterns you see in the coordinates of the points:
Values of coordinates DO NOT change however the signs change according to the CAST rule
Okay, that's all for now. Thanks for reading!
The formula s=rθ can measure the arc length of a circle.
But, the angle MUST be measured in radians (if it's in degrees you'll have to convert it) and the arc length and the radius must be in the same units.
Example:
If the arc length is 81 cm and the radius is 27 cm, find the measure of the central angle to the nearest tenth of a degree.
Equation:
s=rθ
radius = 27 cm
S= 81 cm
1)Manipulate the equation to find the angle
s=rθ
θ=s/r
2) Plug in the variables
θ=81cm/27cm
θ= 3 radians
3) convert radians to degrees
3 (180 degrees/ π)
=171.8873385 dgr
=171.9 dgr
The Unit Circle
-has its centre at the origin
-has a radius of unit 1
-standard position starts at (1,0)
Equation of a unit circle:
x^2+y^2=1
What is positive distance?
Measured in counterclockwise direction
Negative Distance?
Measured in Clockwise direction
What is P(θ)?
-It is used to indicate where the terminal arm intercepts the unit circle.
- every arc length on the unit circle has a unique P(θ)
-P(θ) can also be defined as P(x,y)
SIN, COSIN, TANGENT on the unit circle
On the unit graph:
the y-axis = sin
x-axis=cos
P(θ)= (x,y) = (cosθ, sinθ)
Remember if r=1
sinθ=o/h = y/1=y
cosθ=a/h=x/1=x
tanθ=o/a=tanθ=y/x=sinθ/cosθ
therefore, P(x,y)=P(cosθ, sinθ) and since x^2+y^2=1 then cos^2+sin^2=1
Note: This equation is for a circle with centre at the orgin and a radius other than 1 would be x^2+y^2=r^2
CAST RULE:

CAST rule can help us identify which trigonometric function is positive at each quadrant.
EXAMPLE: Given that sinθ=-4/5 and cosθ=3/5 in which quadrant does θ lie?
Remember the CAST rule, if sinθ is negative and cosθ is positive than then θ must lie in quadrant 4.
Example 3: Determine the expression of the circle with centre at the origin and the radius of 2.
Remember, if the radius is bigger than 1 the equation becomes x^2+y^2=r^2.
x^2+y^2=4
Special Right Triangles:
Determining the exact values of trigonometric ratios of any multiples of 0 dgr, 30 dgr, 45 dgr, 60 dgr, 90 dgr.
There is a trick from India to remember the trigonometric ratios for special right triangles:
0 1 2 3 4
√0/4 √1/4 √2/4 √3/4 √4/4
sinθ 0 1/2 √2/2 √3/2 1
cosθ 1 √3/2 √2/2 1/2 0
tanθ 0 1/√3 1 √3 0 (UNDEFINED)
QUADRANTAL ANGLES

Example : Multiples of π/3
a. on a diagram of the unit circle, show the integral multiples of π/3 in which can be bigger and equal to zero or smaller than or equal to 2π
Note: 3π/3 does not count because it can reduced so it is NOT an integral multiple
b. what are the exact coordinates of each point P(theta) in part a
P(π/3)=(1/2, root 3/2)
(Cast rule so values are positive in Q1)
P(2π/3)= (-1/2, r3/2)
(Cast rules so cosin is negative Q2)
P(4π/3)=(-1/2,-r3/2)
(Cast rule so all values are negative in Q3)
P(5π/3)=(1/2, -r3/2)
(Cast rule so sin is negative in Q 4)
c.Identify any patterns you see in the coordinates of the points:
Values of coordinates DO NOT change however the signs change according to the CAST rule
Okay, that's all for now. Thanks for reading!
No comments:
Post a Comment