um sum and difference identities by marc

SUM AND DIFFERENCE IDENTITIES
This is Marc Valino.
Sum and Difference identities is used to show how to find sine, cosine, or tangent of the sum or difference of two given angles.

You can use these 3 formulas to find out the sum identity of sin, cos, and tan of two given angles.

These 3 are used to find the difference identity of sin, cos, and tan of two given angles.

Example:

To determine exact trigonometric values for angles it is the same concept as above but there is one extra step.

Example:

THE END.

Trigonometric Identities Intro

What is up y'all. Today first thing in the morning we learned about trigonometric Identities.

First off the definition of trigonometric function is an equation that involves at least one trigonometric function of a variable. This equation is referred to trigonometric identity when all permissible values of the variable for which both sides of the equation are shown.

To verify an identity: you show that the left hand side (LHS) is identical to the right hand side (RHS)

Reciprocal Identities:

cscΘ = 1÷sinΘ          secΘ= 1÷cosΘ          cotΘ=1÷tanΘ

Quotient Identities:

tanΘ=sinΘ÷cosΘ          cotΘ=cosΘ÷sinΘ

Pythagorean Identity:

cos² Θ + sin² Θ =1


Example 1. We can verify a potential Identity by..

a) Determining the non-permissible values, in degrees, for the equation secΘ = tanΘ÷sinΘ

We can start on the LHS, follow the steps!
             
               secΘ = tanΘ÷sinΘ

1.

secΘ = 1÷cosΘ         • cos≠ 0
                                             Θ≠ 0°, 90°, 270°
                                             Θ≠ 180°n. where n E I

2.

tanΘ÷sinΘ                • sin≠ 0
                                           Θ≠ 0°, 180°, 360°
                                           Θ≠ 180°n, where n E I

3. 

tanΘ = sinΘ÷cosΘ    • cos≠ 0
                                             Θ≠ 0°, 90°, 270°
                                             Θ≠ 180°n. where n E I

4.

90°n, where n E I

b) Numerically verify that Θ =60° and Θ = π÷4 are solutions of the equation.

1. Θ = 60°

secΘ = tanΘ÷sinΘ

sec60° = tan60°÷sin60°

2. Input perfect right triangles.


2 = √3÷√3÷2

2 = √3 • 2÷√3

2 = 2 

this shows that Θ = 60° is a solution to the equation.

Example 2: Use identities to simplify expressions.

a) Determine he non-permissible values, in radians, of the variable in the expression 
sec x÷tan x.











b) Simplify the expression.

 

Example 3. Pythagorean Identity.

a) Verify that the equation 1 + tan² Θ = sec² Θ is true when Θ = 3π÷4











b) Express the Pythagorean identity cos² Θ + sin² Θ = 1 as the equivalent identity 1 + tan² Θ = sec² Θ.














That is all happy precal-ing!











                   

Graphing Sine and Cosine Functions

Hey everyone!!
I'm going to try and explain graphing sine & cosine functions to you and hopefully it helps!!

Here are some points that will be helpful to understand graphing sine and cosine functions.

• Graphing on a Cartesian plane is known as "unrolling" the Unit Circle.
• Plot theta values on the x-axis and the trigonometric function values at theta on the y-axis
• One cycle is a portion of the graph from one point to another at which time the graph begins to repeat itself.
• One period is the length of one cycle in either degrees or radians. The period for a sin x or cos x function is 2pi/[b]. The period for a tan x function is pi/[b].
• The amplitude is the distance from the middle axis to the highest or lowest point for a sin x or cos x function. A change in amplitude vertically stretches or compresses the basic shape of the curve. The amplitude for sin x of cos x function is (a).  The amplitude for a tan x function is unlimited or infinite

                 Amplitude= max-min/2 

• Basic equations: y = a sin bx and y = a cos bx 
• X represents theta values and y represents the trigonometric function's value at theta.

Examples:

This problem is a combination of dealing with the values of A and B.  The A value of 3 tells us that the graph will have a vertical stretch and the amplitude will be 3.  The B value of 1/2 tells us that a complete cycle of the graph will require more than the standard domain of  0 to (there will be a horizontal stretch).
The period of this new graph will be (or 720º).

 

This problem is also a combination of dealing with the values of A and B.  The A value of 1/2 tells us that the graph will have a vertical shrink and an amplitude of 1/2.  The B value of 3 tells us that 3 complete cycles of the graph will be seen in the standard domain of  0 to (there will be a horizontal shrink).
The period of this new graph will be (or 120º).

 

 

 I hope this helps anyone if someone is struggling!! See you guys in class :)

Trigonometric Equations :)

#LlarcGrad2015

Hello everybody so I'm going to explain how to solve trigonometric equations!

When you're solving trig equations you're basically looking for the values of an unknown angle. The domain will always be 0°≤θ≤360° or 0≤θ≤2π unless otherwise stated. Ultimately we're always going to be solving for θ(theta).

In order to solve trigonometric equations you need to know the CAST rule, the unit circle, the special triangles, SOH CAH TOA, and the quadrantal angles. You need to put all this together to be able to solve trig equations. 

Unit circle

CAST rule

The steps to solve for θ:

1. isolate the trig ratio
2. find the reference angle
3. determine in which quadrant(s) the angle lies
4. check the interval given
5. state final answer(s) for θ in degrees or radians.

Okay so now we're going to solve an example question by following the 5 steps! 


Solve: 2sinθ+ √3=0 , π/2≤θ≤ 3π/2. 

Setp 1: isolate the trig ratio

Okay so the first step to solving this equation is to isolate sinθ. To do this we subtract √3 from both sides of the equation.

2sinθ+ √3=0 

2sinθ+√3-√3 =0-√3

        

             2sinθ=-√3

Now we perform the opposite operation and divide both sides of the equation by 2.

2sinθ+ √3=0 

2sinθ+√3-√3 =0-√3

        

            (2sinθ)÷2 =(-√3)÷2

                    sinθ=-√3/2

Step 2: find the reference angle

To find the reference angle first we determine where sin=√3/2 on the unit circle.  

The coordinates of a unit circle tell us that x=cos and y=sin. 

By looking at the unit circle, we can tell that sin=√3/2 in quadrants 1 and 2. 

Therefore, our reference angle will be 

located in those quadrants. 

In this case, our reference angle is π/3. 

Step 3: determine in which quadrant(s) the angle lies

To determine in which quadrant the angle lies, we look at the sign of sinθ. Whether it's positive or negative indicates where our angle lies. 

sinθ=-√3/2  Here, sine theta equals negative root three over two. Using the CAST rule,
                          we are able to determine that sine is negative in quadrants three and four. 
                          Therefore, our angles will lie in those quadrants.

Now we solve for theta! 

Q III     θ= π + π/3                                                        Q IV     θ= 2π - π/3

              θ= π/1 + π/3                                                                   θ= 2π/1 - π/3

              θ=(π/1) x 3 + π/3                                                           θ=(2π/1) x 3 - π/3

              θ=3π+π/3                                                                        θ= 6π-π/3

              θ=4π/3                                                                             θ= 5π/3

So we have θ= 4π/3, 5π/3. Next we need to check the interval so we end up with one answer 

for θ. 

Step 4: check the interval given

In our question 2sinθ+ √3=0 , π/2≤θ≤ 3π/2, the interval we're provided with is 

π/2≤θ≤ 3π/2. Our final answer has to satisfy the domain. 

                      θ= 4π/3 ✓             θ= 5π/3 X

θ= 5π/3 is rejected because of the restriction on the domain. 

Step 5. state final answer(s) for θ in degrees or radians

θ= 4π/3

Voila! That's how you solve a trigonometric equation! :) 

Trigonometric ratios

Heya guys, so this is the second time I am typing this blog, because the first time I typed this blog, I lost it, even though I pressed save but for some reason I couldn't find it. So, I am just really pi***d off right now, excuse my language Mr.P, but I am just really annoyed. Anyway, lets just get to it, shall we.

So, the first thing that Mr.P taught us was special patterns, but unfortunately I will not be able to explain that to you guys, because when Mr.P was teaching us about the two special patterns, I kind of zoned out. However, I did ask Heba Abbas to explain the two special patterns, but I guess she just didn't want to it, that is why she didn't show up at the library during our spare, to explain the special patterns to me, so I guess we can all blame her for not having special patterns on my blog, just kidding. But, whenever I understand the special patterns, I will make  blog about it later.

So.. moving on to Trigonometric ratios:

If P(theta) = (x,y) is the point on the terminal arm of angle theta that intersects the unit circle, notice that, P(theta) = (x,y) = (cose theta, sin theta), so the x- axis in cose, and the y-axis in sine.

If r = 1, then

1. sin theta = O/H, which is that same as y/1, and that equals to y. Then, csc theta is the inverse of the sin theta ratio, so csc theta = H/O = 1/sin theta.
2. Cos theta = A/H, which is the same as X/1, and that equals to x. Then, sec theta is the inverse of cos theta, so sec theta = H/A = 1/cos theta
3. Tan theta = O/A, which is the same as y/x, and tan theta = sin theta/cos theta. Then, cot theta is the inverse of tan theta, so cot theta = A/H = cos theta/sin theta.

Therefore, P(x,y) = P(cos theta, sin theta), and, since x^2 + y^2 = 1, we have a Pythagorean identity, cos^2 theta + sin^2 theta = 1.

Example: The point A(-1/3, -2/3) lies at the intersection of the unit circle and the terminal arm of an angle theta in standard position.

• The first step, would be to draw a diagram like I did above. Point A, is in quadrant three, because cos theta and sin theta, are negative, which means opposite and adjacent are negative, and both of them are negative in quadrant three. 
• The second step, would be to label the diagram, so place the opposite, adjacent, and hypotenuse values on the the triangle. So, -1 will go on the x-axis, cos theta, adjacent side, -2 will go on the y-axis, sin theta, opposite side, and 3 will go on the hypotenuse side.
• The third step, is to determine the values of the six trigonometric ratios for theta. Express answers in lowest terms.

Trig ratios:

Sin theta = O/H = -2/3

Cos theta = A/H =  -1/3

Tan theta = O/A = -2/3

Csc theta(inverse of sin theta) = H/O = 3/-2

Sec theta(inverse of cos theta) = H/A = 3/-1 = -3

Cot theta(inverse of tan theta) = A/O = 3/-2

Determining exact values of trigonometric equations:

Example: cos 5 pi/6

  

Step-by-Step solution:

1. First draw a diagram like above. Then, according to the unit circle, 5 pi/6 is 150 degrees, and then since 5 pi/6 is positive, it will go clockwise. 
2. Then, determine the reference angle. Now, there are three ways you an determine the reference angle.

• The first way, is subtracting 150 from 180, since theta is approaching the 180 degrees axis. So, you will get a reference angle of 30 degrees
• The second way, is splitting the cos 5 pi/6 into two. So, it will be 4pi/6 = 2pi/3, and pi/6, since 4pi/6 + pi/6 = 5 pi/6. So, pi/6 will be your reference angle, which is 30 degrees according to the unit circle
• The third way, is probably the simplest, which is just ignoring the fact that there is a 5 in front of pi, which leaves you with pi/6 = 30 degrees. So, your reference angle would be 30 degrees.

3. After you determined the reference angle,you should know what type of special triangle it is. In this case, we have 30 -60-90 degrees triangle, since our reference angle is 30 degree. Next, we jut label the sides of the special triangle. So, the side opposite the 30 degree angle will have 1. The 60 degree angle, the second biggest angle will have square-root of 3 on the adjacent side, and the biggest angle, 90 degree will have two on the hypotenuse.

4. Next, apply the cast rule, and put a negative sign in front of square-root 3

5. Lastly, Cos theta = A/H, so - sqaure-root of 3/2

Ok, I am tired of blogging now, so I will do part two tomorrow. See you in class tomorrow guys, bye for now. :D

Hello! This is Heba on the world’s slowest computer to explain the key concepts in the Circular Function unit. 

Arc Length

S= Arc Length

r= radius

θ= angle MEASURED IN RADIANS

The formula s=rθ can measure the arc length of a circle. 
But, the angle MUST be measured in radians (if it's in degrees you'll have to convert it) and the arc length and the radius must be in the same units.

Example:

If the arc length is 81 cm and the radius is 27 cm, find the measure of the central angle to the nearest tenth of a degree.

Equation:
s=rθ
radius = 27 cm
S= 81 cm

1)Manipulate the equation to find the angle 
 s=rθ
θ=s/r

2) Plug in the variables
θ=81cm/27cm
θ= 3 radians

3) convert radians to degrees
3 (180 degrees/ π) 
=171.8873385 dgr
=171.9 dgr

The Unit Circle




-has its centre at the origin
-has a radius of unit 1
-standard position starts at (1,0) 
Equation of a unit circle:
x^2+y^2=1

What is positive distance?
Measured in counterclockwise direction 
Negative Distance?
Measured in Clockwise direction

What is P(θ)? 
-It is used to indicate where the terminal arm intercepts the unit circle. 
- every arc length on the unit circle has a unique P(θ)
-P(θ) can also be defined as P(x,y)

SIN, COSIN, TANGENT on the unit circle 



On the unit graph:
the y-axis = sin
x-axis=cos
P(θ)= (x,y) = (cosθ, sinθ)

Remember if r=1
sinθ=o/h = y/1=y
cosθ=a/h=x/1=x
tanθ=o/a=tanθ=y/x=sinθ/cosθ

therefore, P(x,y)=P(cosθ, sinθ)  and since x^2+y^2=1 then cos^2+sin^2=1

Note: This equation is for a circle with centre at the orgin and a radius other than 1 would be x^2+y^2=r^2


CAST RULE:


CAST rule can help us identify which trigonometric function is positive at each quadrant.

EXAMPLE: Given that sinθ=-4/5 and cosθ=3/5 in which quadrant does θ lie?
Remember the CAST rule, if sinθ is negative and cosθ is positive than then θ must lie in quadrant 4.

Example 3: Determine the expression of the circle with centre at the origin and the radius of 2.
Remember, if the radius is bigger than 1 the equation becomes x^2+y^2=r^2.
x^2+y^2=4

Special Right Triangles:
 Determining the exact values of trigonometric ratios of any multiples of 0 dgr, 30 dgr, 45 dgr, 60 dgr, 90 dgr.




There is a trick from India to remember the trigonometric ratios for special right triangles:
     
            0               1                2        3            4
            √0/4          √1/4          √2/4    √3/4        √4/4 
sinθ      0                1/2           √2/2    √3/2        1
cosθ     1                √3/2         √2/2   1/2          0
tanθ      0                1/√3           1       √3         0 (UNDEFINED)


QUADRANTAL ANGLES





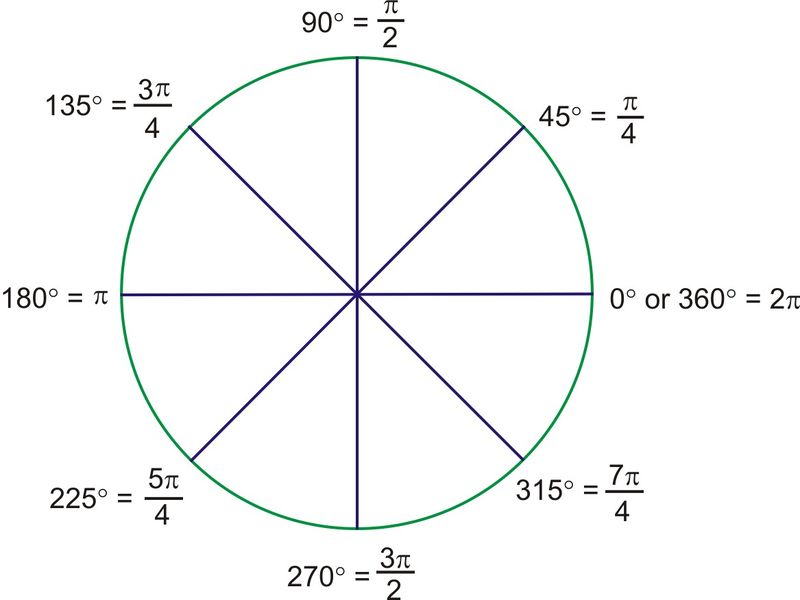
Example : Multiples of π/3
a. on a diagram of the unit circle, show the integral multiples of π/3 in which can be bigger and equal to zero or smaller than or equal to 2π

Note: 3π/3 does not count because it can reduced so it is NOT an integral multiple

b. what are the exact coordinates of each point P(theta) in part a
P(π/3)=(1/2, root 3/2)
(Cast rule so values are positive in Q1)
P(2π/3)= (-1/2, r3/2)
(Cast rules so cosin is negative Q2)
P(4π/3)=(-1/2,-r3/2)
(Cast rule so all values are negative in Q3)
P(5π/3)=(1/2, -r3/2)
(Cast rule so sin is negative in Q 4)

c.Identify any patterns you see in the coordinates of the points:
Values of coordinates DO NOT change however the signs change according to the CAST rule



Okay, that's all for now. Thanks for reading!