Hi everyone! Minako here and going to talk about Degree and Radian Measure.
Radian and Degree are two units for measuring angles.

Initial side- is the starting point of the ray.
Terminal side- is where an angle stops.
If the rotation is positive then it is in clockwise direction
If the rotation is negative then it is in counter-clockwise direction.

Whenever radius is equal to its arc length, then theta will always be equal to 1 radian.
Whenever radius is not equal to arc length, then theta will be greater or lesser then 1 radian.
To convert degrees to radian
multiply degrees to Π/180 degrees
example: 270 degrees
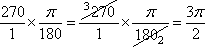
To convert radian to degrees
multiply radian to 180/Π
Radian and Degree are two units for measuring angles.
Initial side- is the starting point of the ray.
Terminal side- is where an angle stops.
If the rotation is positive then it is in clockwise direction
If the rotation is negative then it is in counter-clockwise direction.
Whenever radius is equal to its arc length, then theta will always be equal to 1 radian.
Whenever radius is not equal to arc length, then theta will be greater or lesser then 1 radian.
To convert degrees to radian
multiply degrees to Π/180 degrees
example: 270 degrees
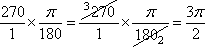
To convert radian to degrees
multiply radian to 180/Π
example: Π/6
COTERMINAL ANGLES
-Two angles are coterminal if they are drawn int he standard position and both have their terminal sides in the same location.
Finding the positive coterminal angles:
Just add 360 degrees to the angle given.
(add 2Π if the given is in radian)
Finding the negative coterminal angles:
Just subtract 360 degrees to the angle given.
(for degrees higher than 360, subtract another 360 until the angle turns negative)
(subtract 2Π if the given is in radian)
QUADRANTAL ANGLES:
-An angle with the terminal side on the x-axis or y-axis.
That is, the angles of 0°, 90°, 180°, 270°, 360°, 450°, ... as well as –90°, –180°, –270°, –360°, ...